Some Quick Notes:
- Training has been completed
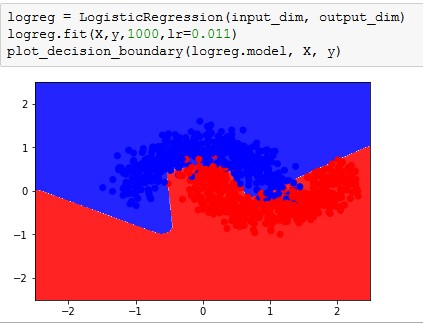
- No, the two layer neural net cannot model non-linear decision boundaries as the system deals simply with coefficients of linear variables. This indicates that the feedback necessary for non-linear models cannot be met; it is limited to a linear model.
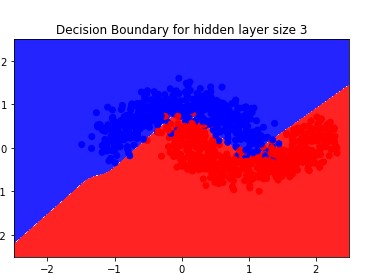
- Yes, the 3 layer model can learn non-linear decision boundaries as the hidden layer enables higher order representations like curves. Practically the hidden layer allows further feedback, creating compounded activations, akin to creating non-linear variables.
- Learning rate affects the aggressiveness of training; Lower rates yield better training, but longer processing time. Higher rate result in
- Smaller gradient (0.001)
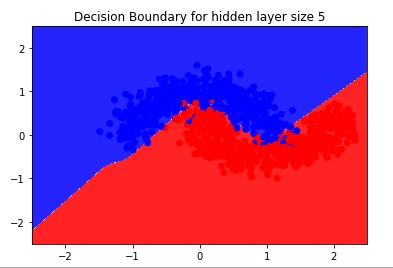
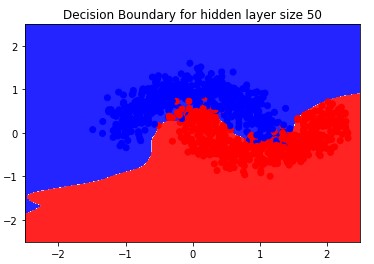
- Changing the amount of hidden nodes changes the complexity of the curve; More nodes results in a curve with more local minimas or maximas (or in plain English: bendiness)
- What is overfitting & why does it occur?
- Overfitting is when the error on a training set is low, but the error rate on new data is high. It occurs
- What are
three solutions?
- What are three possible solutions?
- The first solution is to simply increase the size and variation of the training data set. It’s a really straightforward process, as it just increases the inputs.
- The next two methods work on biasing data towards a specific solution:
- The second possible solution is L1 regularization, which attempts to make the fewest amounts of inputs have non-zero weights. This is commonly is known as creating a sparse solution.
- The third possible solution is L2 regularization. This solution differs from L1 because it can be calculated analytically. It biases by using the square of the magnitude of the difference.
- L2 Regularization is a weight decay linearization. This process attempts to use as many nodes as it can, thereby creating small weights. This process created significantly more jagged edges, but ultimately increased the accuracy. (As an FYI, this is my approximation, I had l2 regulation encoded as default)